Sho Tsugawa's Homepage:情報メディア実験

目次

次数分布

  • ノードに接続されているリンクの数 (次数) の分布

次数分布

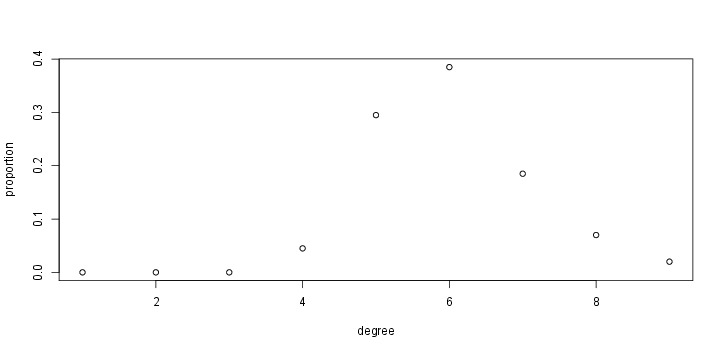
ER モデルによって生成したグラフの次数分布

R で次数分布をプロットする方法

> library(igraph)
> g<-erdos.renyi.game(n=200,p=0.05)
> dd<-degree.distribution(g) # 次数分布を求める
> plot(dd[-1],xlab="degree",ylab="proportion") # 次数分布をプロットする
> plot(dd[-1],log="xy",xlab="degree",ylab="proportion") # 両対数軸でプロットする

Excel や gnuplot などのツールを用いてプロットする方法

> dd<-degree.distribution(g) # 次数分布を求める
> write.table(dd[-1],"distr.txt",quote=F,col.names=F) #distr.txt というファイルに次数分布を出力
> d<-degree(g) #各ノードの次数を求める
> write.table(d,"degree.txt",quote=F,col.names=F) #degree.txt というファイルに各ノードの次数を出力

集計した値がほしければ、distr.txt を、各ノードの次数がほしければ degree.txt を Excel や gnuplot で読み込めばよい。

平均経路長

  • ノード間の最短経路長の平均

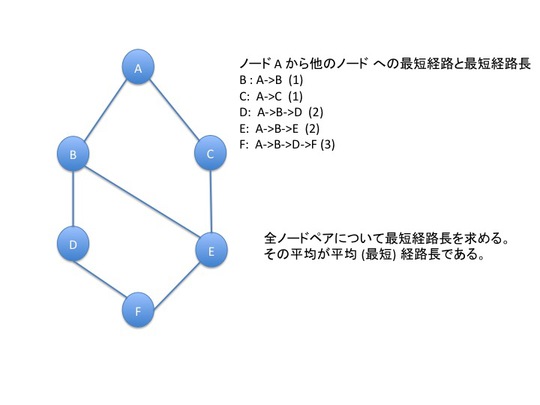
Shortest Path

R による平均経路長の計算

平均だけ求めたい場合は、以下のコマンドを実行すればよい 

> average.path.length(g)

各ノードペアの最短経路長を求めたい場合は以下のコマンドを実行すればよい 

> D<-shortest.paths(g) 
> D[1,200] # ノード 1 とノード 200 の最短経路長

クラスタリング係数

グラフ中に存在する三角形の割合。正確には、クラスタリング係数 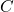$C$ は

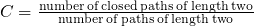
$C=\frac{{\rm number \, of \, closed \, paths \, of \, length \, two}}{{\rm number \, of \, paths \, of \, length \, two}}$

のように定義される。いくつかの定義が存在するが、意味することは同じである。ソーシャルネットワークにおいては、クラスタリング係数が高いほど、友人の友人が友人である確率が高いといったことを意味する。

R による計算方法

> transitivity(g)

日付: 2014-10-01T19:40+0900

著者: Sho Tsugawa

Validate XHTML 1.0